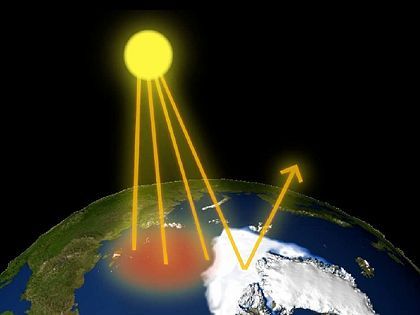Albedo

Albedo ("Weißheit"; von lateinisch albus: "weiß") bezeichnet das Rückstrahlvermögen von nicht selbst leuchtenden Oberflächen. In der Meteorologie ermöglicht die Albedo Aussagen darüber, ... [mehr]

Buhne

Eine Buhne ist ein dammartiges, quer zur Uferlinie angelegtes Regelungsbauwerk, womit der durchflußwirksame Querschnitt eines Gewässers eingeschränkt wird. Buhnen werden angelegt, um für die Schiffahrt ... [mehr]

Chott

Ein Chott ist eine Salzton-Ebene in der Wüste Sahara, vorwiegend in Tunesien, Algerien und Marokko. Die Salzseen bleiben im Sommer trocken, nehmen aber im Winter Wasser auf. Sie haben wechselnde Küsten ... [mehr]

Desertifikation

Die Desertifikation oder auch das "Sahel-Syndrom" (vom lateinischen "desertum facere" gleich „wüst machen“ oder „verwüsten“) bezeichnet die Verschlechterung des Bodens in relativ trockenen (ariden und semiariden) ... [mehr]

Enklave

Eine Enklave ist ein Staatsteil eines Landes, der vollständig in einem anderen Staat liegt. Dieser Teil hat somit keine Verbindung zum größeren Teil des eigenen Staates. Umgekehrt ist dieser Landesteil eine Exklave ... [mehr]

Fairtrade

Mit dem Begriff "Fairtrade" werden die Aktivitäten, Organisationen und Vertragswerke umschrieben, die den Handel zwischen den Industriestaaten und den Entwicklungsländern so gestalten ... [mehr]

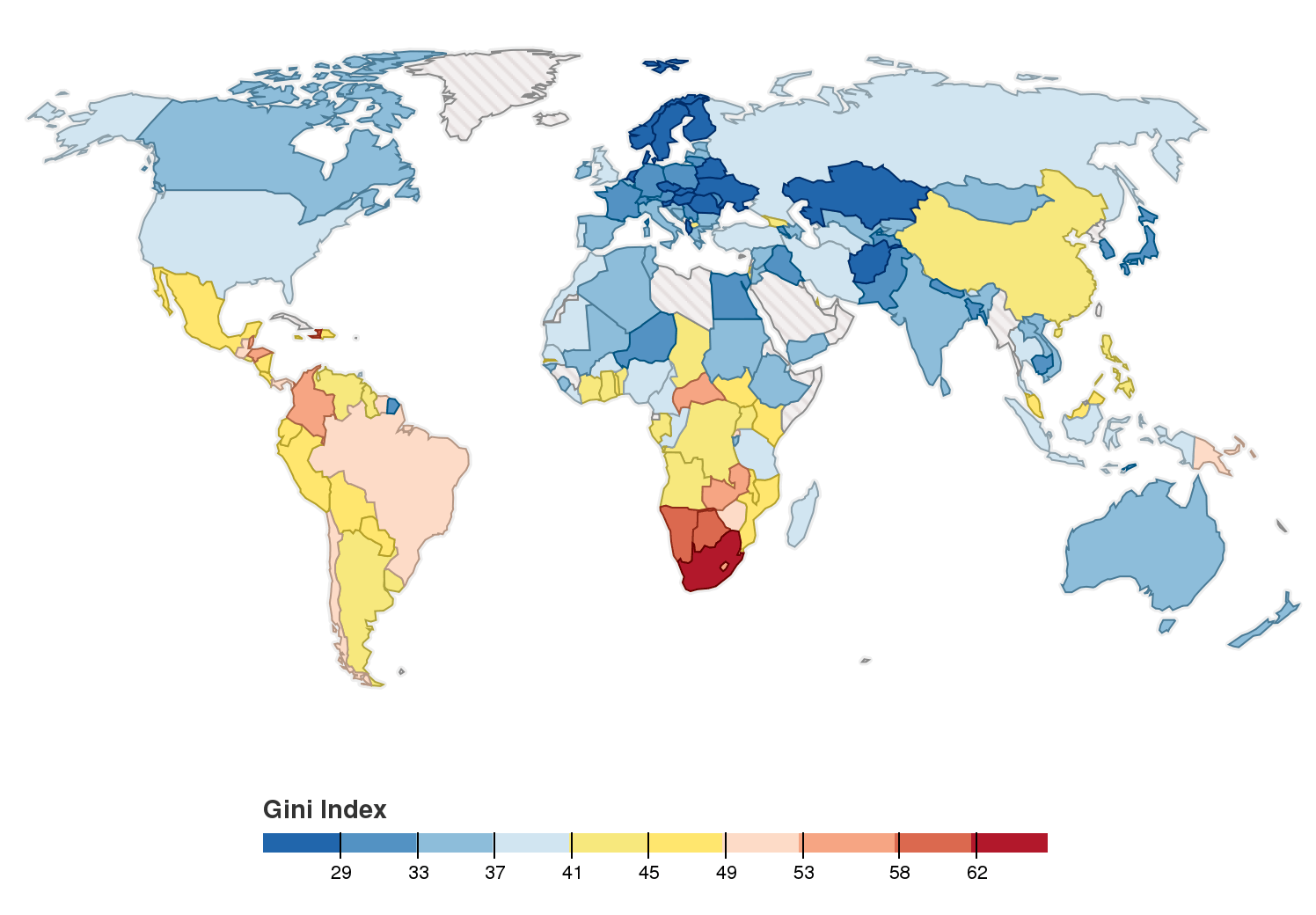Gini-Koeffizient

Der Gini-Koeffizient gibt den Grad der Ungleichheit der Einkommensverteilung in einem Land oder einer Region an. Die Berechnung des Gini-Koeffizienten geht aus der Lorenz-Kurve hervor ... [mehr]

Löss

Löss ist ein gelbliches, poröses, sehr feinkörniges und kalkhältiges Staubsediment, das in der Eiszeit aus den Schotterterrassen der großen Flüsse angeweht wurde. In Österreich wurden große Teile des Weinviertels ... [mehr]

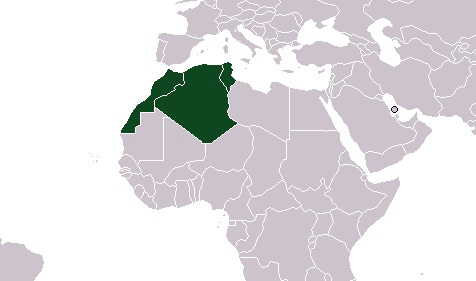Maghreb

Maghreb ist ein Sammelbegriff für eine Region und bedeutet auf arabisch "Westen". Zu den Maghrebstaaten zählen die westlichsten Länder unter muslimischer Herrschaft in Nordafrika, darunter vor allem die Region ... [mehr]

NUTS

NUTS ist eine französische Abkürzung für "Nomenclature des unités territoriales statistiques". NUTS ist die hierarchische Gebietsgliederung der EU, die NUTS-Hierarchien sind sind durchnummeriert. Die NUTS-Regionen ... [mehr]

Wadi

Wadi ist sowohl eine Bezeichnung für einen ausgetrockneten Flusslauf, der nur nach starken Regenfällen vorübergehend Wasser führt als auch eine Bezeichnung für ein tiefes, steilwandiges, gewöhnlich zirkusförmig ... [mehr]

Zenit

Der Zenit ist der Schnittpunkt zwischen der senkrechten Achse über einem bestimmten Ort und der Himmelsphäre. Für einen Betrachter stellt der Zenit den aus seiner Sicht höchsten Punkt des Himmels dar − dieser Punkt befindet ... [mehr]

Corioliskraft

Winde auf der Südhalbkugel werden nach links, auf der Nordhalbkugel nach rechts abgelenkt. Aber warum ist das so ? Dies liegt an der Corioliskraft, für deren Entstehen die Erdrotation verantwortlich ist ... [mehr]

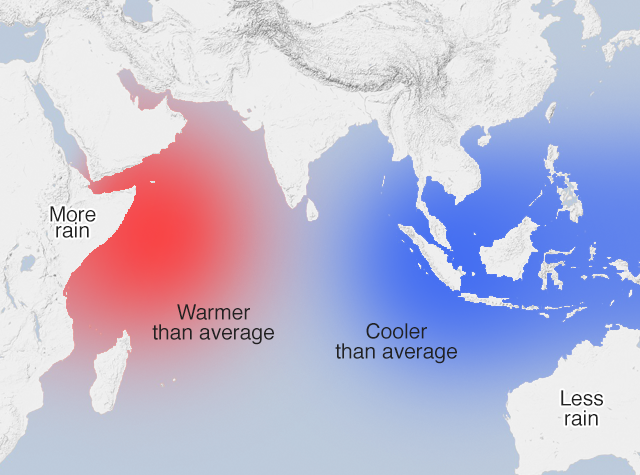Indischer Ozean Dipol

Nicht nur Australien leidet durch Buschbrände unter einem Wetterphänomen. Das gleiche Wetterphänomen, das in Australien zu den Feuern beigetragen hat, sorgt in Ostafrika durch zahlreiche Niederschläge ... [mehr]

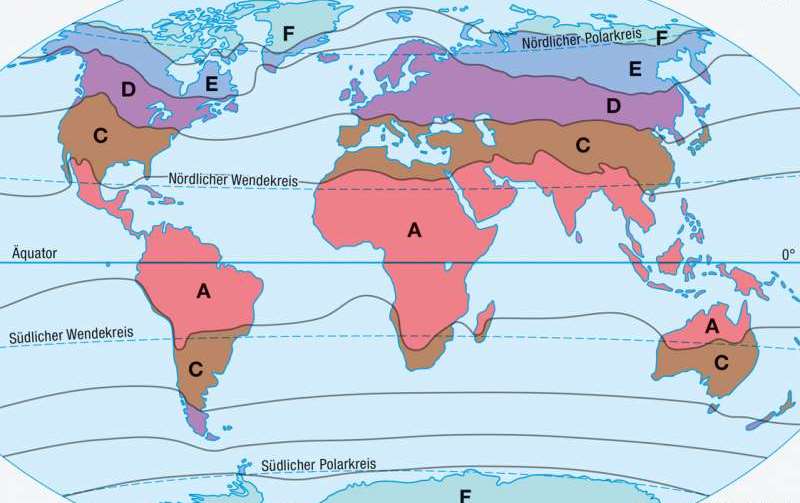Klimazonen

Eine Klimazone ist ein Gebiet mit gleichen klimatischen Bedingungen, das sich bandartig um die Erde zieht. Die Klimazonen der Erde basieren auf den Beleuchtungszonen der Erde. Dabei ergeben sich ... [mehr]

Küstenwüsten

Wüsten, die direkt am Meer liegen, sind eigentlich paradox. Wieso kann sich nahe am Wasser, wo doch genug Feuchtigkeit ist, eine Wüste ausbilden ? Die Ursache für dieses Phänomen liegt ... [mehr]

Medicanes

"Medicanes" ist ein Kunstwort, das aus den Begriffen "mediterranean" und "Hurricane" zusammengesetzt ist. Es bezeichnet Sturmtiefs im Mittelmeerraum, die tropischen Wirbelstürmen ähnlich sind. [mehr]

Singende Dünen

Dünen sind nicht nur eindrucksvolle Fotomotive, sondern sie können auch Töne von sich geben. Marco Polo hat das als einer der ersten Reisenden beschrieben. Die Forschung geht davon aus, dass Dünen ... [mehr]

Sonnenscheindauer

Die Sonnenscheindauer ist die tatsächliche Dauer der direkten Sonneneinstrahlung an einem bestimmten Ort innerhalb eines bestimmten Zeitraumes, d.h. jene Dauer, in der ein Objekt am Erdboden einen sichtbaren Schatten wirft ... [mehr]

Taupunkt

Warme Luft kann aufgrund des höheren Dampfdrucks (dieser hält die in der Luft liegenden Wassermoleküle bzw. Wasserdampfmoleküle zusammen) mehr Feuchtigkeit binden als kalte Luft. Dieser Effekt ist ... [mehr]

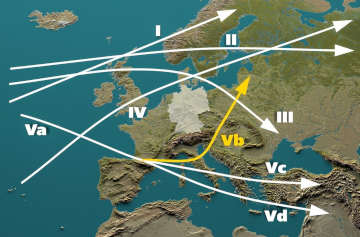V b - Wetterlage

Die geographische Lage von Hoch- und Tiefdruckgebieten, den bedeutendsten Steuerungszentren des Wettergeschehens, wird in der Meteorologie als "Wetterlage" oder "Großwetterlage" bezeichnet. [mehr]

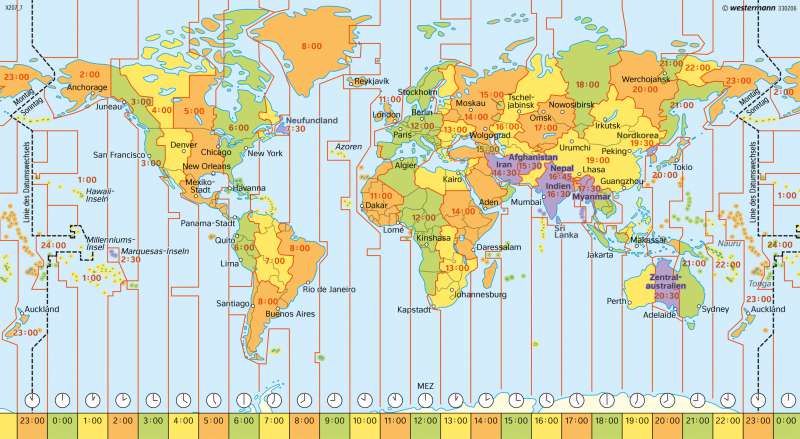Zeitzonen

Ab der Mitte des 19. Jahrhunderts kommt es weltweit zu einer rasanten Ausweitung der Eisenbahn- und Telegraphennetze. Die Globalisierung des Nachrichtenverkehrs durch das ... [mehr]

Keine Überraschung

Die ungewöhnlich starke Erwärmung der Meere in den vergangenen zwei Jahren war laut einer neuen Studie nicht unvorhersehbar. Ein seltenes Extremereignis habe dazu geführt. Nicht nur für Fachleute ist das ...[mehr]

Verstärkung

Starkregenereignisse sind in Österreich in den vergangenen 40 Jahren intensiver geworden. Vor allem kurzfristige Extremniederschläge haben aufgrund der Klimaerwärmung stark zugenommen − auch kleinräumige ...[mehr]

Notbremse

Die Demokratische Republik Kongo (DRK) ist der mit Abstand größte Exporteur von Kobalt. Ein Auge darauf geworfen haben auch Rebellenmilizen, die sich im rohstoffreichen Osten vorkämpfen. Inzwischen wird in den zahllosen ...[mehr]

Modell Atacama

In der extrem trockenen Atacama−Wüste in Südamerika könnte Nebel eine neue Wasserquelle sein. Eine Studie zeigt, dass spezielle Kollektoren täglich mehrere Liter Wasser pro Quadratmeter gewinnen könnten.[mehr]

Mehr Mikroplastik

Eine von Greenpeace in Auftrag gegebene Analyse hat in allen untersuchten Gletscherseen in Österreich Mikroplastik nachgewiesen. Die Proben wurden im Sommer auf der Pasterze, dem Osttiroler Schlatenkees ...[mehr]

Unterbelichtet

Der Fiskalrat hat in einer Studie die klimapolitische Strategie in Österreich hinsichtlich ihrer Kosteneffektivität bewerten lassen. Den öffentlichen Ausgaben für die Maßnahmen wurde ihr Potenzial zur Vermeidung ...[mehr]

Das Wesen der Wüste

Unendliche Weite, einzigartige Schönheit, nahezu unberührte Natur – seit mehr als 35 Jahren bereist der Abenteurer, Fotograf und Geograf Michael Martin die Wüsten der Erde und entdeckt immer wieder ... [mehr]

Der lachende Kontinent

Die größte Kirche der Welt steht in der Elfenbeinküste, in Äthiopien gibt es guten Wein und der schönste Ort Kenias ist ein Hubschrauberlandeplatz über den Dächern Nairobis. Es sind Orte, die man ... [mehr]

Die 101 w. Fragen − Die EU

Der Einigungsprozess Europas hat einem über Jahrhunderte hinweg vom Krieg zerfleischten Kontinent eine inzwischen sieben Jahrzehnte währende Friedensphase beschert. Den meisten Europäern ... [mehr]

Die Macht der Geographie

Die Geographie hat die politische und gesellschaftliche Entwicklung der Völker stets geformt. Dazu gehören Landschaft und Klima, aber auch Demographie, Kulturräume und der Zugang zu natürlichen Ressourcen. [mehr]

Die neue Arktis

"Wenn früher einer im Winter starb, konnte man ihn erst im Juni beerdigen, weil man vorher gar kein Grab ausheben konnte. Jetzt müssen wir die Toten zu einem Notfriedhof weiter im Inland bringen, in der Tundra. [mehr]

Fetzblau oder Schnieseln

Der bekannte österreichische Wettermoderator aus Rundfunk und Fernsehen Sigi Fink zeigt, wie jeder von uns mit einfachen Regeln das Wetter vorhersagen kann: durch gewiße Wolkenarten oder Wetterphänomene ... [mehr]

Gebrauchsanweisung USA

Die USA sind ein Land, das täglich neu überrascht, zum Lachen bringt, verärgert und fasziniert. Der Autor weiß, warum Gott ein Amerikaner ist und was die Menschen zwischen Orlando und Seattle tatsächlich ... [mehr]

Klimawandel

Marcus Wadsak ist einer der bekanntesten Klimawandel-Experten im österreichischen Journalismus. Mit dem Buch "Klimawandel – Fakten gegen Fake & Fiction" liefert er ein Erklärbuch zu diesem Thema. Dabei werden ... [mehr]

Weltmacht China

Das chinesische Wort für "Kommunismus" können sie kaum aussprechen, und während die jungen Starbucks-Gäste im Pekinger Viertel Sanlitun die "Xi-Jinping-Gedanken" auswendig gelernt haben, ... [mehr]

Austria − A Great Place To Live

I love living in Austria and feel privileged to be able to do so. I love the people, the scenery, the healthcare system and most of all the feeling of safety − which none of us should take for granted. lt doesn´t matter ... [more]

Brexit

I am in England at the moment and, in my opinion, there is really only ONE positive thing about Brexit and that is that the newspapers always have something to write about. lt doesn´t matter which one you buy ... [more]

Fight Poverty

Ask Americans whether they want to spend taxpayer money to educate girls abroad, and 80 percent say yes. Do they want to give food and medical assistance in poor countries ? Eighty four percent do. Prevent and treat ... [more]

Solar Lamps

Fighting climate change and poverty simultaneously is the speciality of "green energy against poverty" (greenap), a German NGO based in Bonn. New projects are launched now in poor regions of India on ... [more]

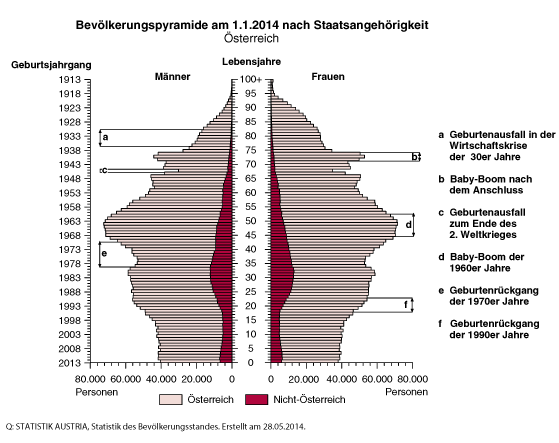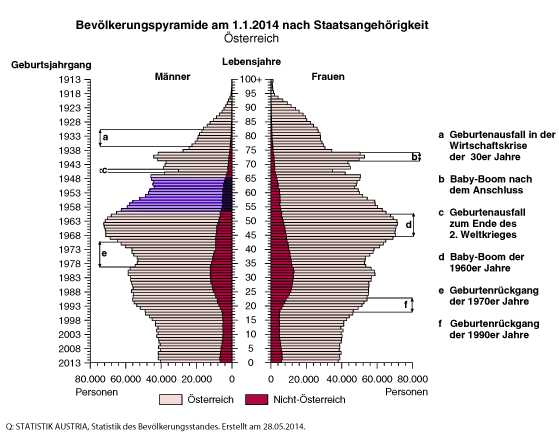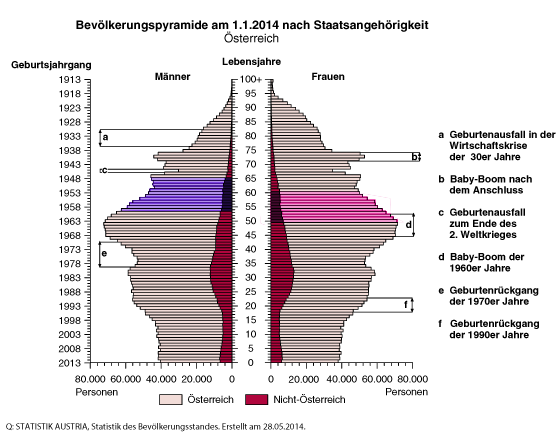Alterspyramiden

Eine Alterspyramide ist eine graphische Darstellungsform des Altersaufbaus einer Bevölkerung. Sie zeigt die Anteile von Männern und Frauen in Jahrgängen oder Altersklassen. Die Anteile können sowohl in ... [mehr]

Gini-Koeffizient

Der vom italienischen Statistiker und Demographen Corrado Gini entwickelte Gini-Koeffizient beschreibt den Grad der Ungleichheit der Einkommensverteilung in einem Land oder einer Region. [mehr]

Glossar

Ein alphabetisch geordnetes Verzeichnis von Fachbegriffen mit Erklärungen, das auf Themengebiete der Geographie und Wirtschaftskunde zugeschnitten ist. [mehr]

Grips

Welches Z wird aus Baumrinde gewonnen und schmeckt gut auf Milchreis ? Wenn Sie ein geographisches Spiel für helle Köpfe mögen, dann sind Sie in dieser Rubrik absolut richtig. [mehr]

Medien

Von A wie dem A-Horizont eines Bodenprofils bis Z wie der Zyklonenfamilie. Hier finden Sie Hinweise zu Sendungen in Hörfunk und Fernsehen, die alle einen geographischen oder einen wirtschaftskundlichen Hintergrund aufweisen. [mehr]

Vitus BERING

Vitus BERING (getauft am 21./31. 8. 1681 in Horsens,† 8. 12. 1741 auf der Beringinsel) war ein dänischer Seeoffizier, der 1703 in der neu geschaffenen russischen Flotte des Zaren Peter I. anheuerte. Er ließ sich in Russland ... [mehr]

George EVEREST

George EVEREST (*4. 7. 1790 in Crickhowell,† 1. 12. 1866 in London) war ein Geodät (Geometer), der sich besonders um die Landvermessung und Kartierung Indiens verdient gemacht hat. Zwischen 1830 und ... [mehr]

Ferdinand MAGELLAN

Ferdinand MAGELLAN (* 3. 2. 1480 in Sabrosa, Portugal; † 27. 4. 1521 auf Mactan, Philippinen) war ein portugiesischer Seefahrer, der 1517 nach Spanien ging. Er wollte im äußersten Süden der Erde eine Ost−West−Passage ... [mehr]

Die Erde

Die Erde ist der dichteste, fünftgrößte und der Sonne drittnächste Planet des Sonnensystems. Sie ist Ursprungsort und Heimat aller bekannten Lebewesen. Ihr Durchmesser beträgt mehr als 12700 km und ihr Alter etwa 4,6 Milliarden Jahre. [mehr]

Europa

Europa ist ein Erdteil, der sich über das westliche Fünftel der eurasischen Landmasse erstreckt. Obwohl geographisch ein Subkontinent, der mit Asien das Gebiet "Eurasien" bildet, wird es meist als eigenständiger Kontinent betrachtet. [mehr]

Österreich

Österreich ist ein Binnenstaat mit rund 8,8 Mio. Einwohnern. Es erstreckt sich in W−E Richtung über maximal 575, in N−S Richtung über maximal 294 km. Rund 60 % des Staatsgebietes haben Anteil an den Ostalpen. [mehr]

Afrika 01

Afrika ist der zweitgrößte Kontinent der Erde, hat mit 54 Staaten die meisten Länder der Erde und mehr als 3 000 Völker mit verschiedenen Sprachen und Kulturen. Auf mehr als 30 Mio. km² leben mehr als 1,2 Mrd. Menschen. [mehr]

Afrika 02

Afrika ist der zweitgrößte Kontinent der Erde, hat mit 54 Staaten die meisten Länder der Erde und mehr als 3 000 Völker mit verschiedenen Sprachen und Kulturen. Auf mehr als 30 Mio. km² leben mehr als 1,2 Mrd. Menschen. [mehr]

Australien

Ein Kreuzworträtsel zum auf der Südhalbkugel nordwestlich von Neuseeland gelegenen und zugleich sechstgrößten Staat der Erde, dessen Name sich vom lateinischen "terra australis" für "südliches Land" ableitet. [mehr]

China

China liegt im Osten Asiens und grenzt an 14 Länder. Es ist das viertgrößte Land der Erde und rund ein Fünftel der Weltbevölkerung lebt in China. Im Westen des Landes liegt der Himalaya, das höchste Gebirge der Erde. [mehr]

Italien

In diesem Rätsel geht es um Begriffe zu einer fast 1200 km langen Halbinsel im Mittelmeer, die auf der Landkarte wie ein Stiefel aussieht und nach dem Gebirge des Appenins auch als "Appenin-Halbinsel" bezeichnet wird. [mehr]

Japan

Der Inselstaat Japan besteht aus einer 2 600 km langen Inselkette, die der Pazifikküste Ostasiens vorgelagert ist. Zu dieser Inselkette gehören 3922 Inseln. Die Küstenlänge aller Inseln beträgt rund 30 000 km. [mehr]

Österreich

Österreich ist ein Binnenstaat mit rund 9,1 Mio. Einwohner*innen und erstreckt sich über rund 570 km von Westen nach Osten. Zwei Drittel des Landes liegen in den Alpen. Acht Staaten grenzen an Österreich. [mehr]

Südamerika

Der viertgrößte Kontinent der Erde liegt zwischen zwei Ozeanen und besitzt die längste überseeische Gebirgskette der Erde. Gleichzeitig findet man sowohl tropische Regenwaldgebiete als auch Wüstenregionen. [mehr]

Folge 1

Ein Überblick

Das Relief Afrikas ist im Inneren des Kontinents großräumig in Becken und Schwellen gegliedert, das Gewässersystem ist auf die Becken ausgerichtet (z.B. Flüsse zum Tschadsee, Kongobecken) und Wadis sowie ... [mehr]

Folge 2

Mitumba

Rund 19 Kilogramm Kleidung werden laut der Umweltschutzorganisation Global 2000 in Österreich pro Person und Jahr gekauft. Herr und Frau Österreicher geben dabei jährlich rund € 9,2 Mrd. aus. Billige ... [mehr]

Folge 3

Brennpunkt Afrika

Ursachen für Afrikas Misere gibt es viele: der Klimawandel, der die Regionen südlich der Sahara zu Wüsten macht; Kriege aus ethnischen Motiven oder wegen wertvoller Rohstoffe; die Kleptokratie von Potentaten ... [mehr]

Folge 4

Polio besiegt

In Europa gilt das Poliovirus bzw. die Poliomyelitis offiziell seit fast zwei Jahrzehnten als ausgerottet, wenngleich einzelne Fälle auftraten, am Dienstag meldete nun auch Afrika entsprechende Erfolge ... [mehr]

Folge 5

Radio als Klassenzimmer

Weltweit ist aktuell rund ein Drittel aller Kinder von Schulschließungen betroffen. UNICEF warnt vor einer "verlorenen Generation". In Ruanda hat man versucht, den Kontakt zu Schülerinnen und ... [mehr]

Folge 1

Jetstreams

Vielfliegern ist der Jetstream ein Begriff. Die kräftige Höhenströmung zieht in Schlangenlinien von West nach Ost. Sie beschert Flugzeugen auf dem Weg von den USA nach Europa Rückenwind und bremst in der Gegenrichtung. [mehr]

Folge 2

Karten zeigen Klimawandel

Klimaerwärmung zu kommunizieren, ist schwierig. Dabei gelten gut aufbereitete Informationen als Schlüssel für präventives Handeln. Österreichische Forscher haben nun regionale Klimakarten erstellt. [mehr]

Folge 3

Blockadewetter

Woher kommt die ungewöhnlich stabile Wetterlage, die in Europa im Sommer 2018 wochenlang für Hitze und Trockenheit sorgte ? Eine wichtige Rolle spielen laut neuen Studien riesige Luftströme in der Atmosphäre ... [mehr]

Folge 1

Wasserverbrauch

Den Österreichern steht viel mehr Wasser zur Verfügung, als sie verbrauchen. Dennoch werden hierzulande − weitgehend unbemerkt − nahezu unvorstellbare Mengen verschwendet. Es gibt leichtere Aufgaben, als ausgerechnet ... [mehr]

Folge 2

Kapstadt und die Dürre

Wie schnell sich das Blatt wenden kann: Wochenlang hatten Horrormeldungen über den "Day Zero" die Berichterstattung über Kapstadt und seine Wasserkrise bestimmt − den Tag, an dem die Wasserversorgung der Vier−Millionen−Stadt ... [mehr]

Folge 3

Der Avocado−Wahnsinn

Es gibt sie in jedem Supermarkt und Discounter. Avocados sind der Trend im Obst− und Gemüseregal. Denn neben dem Geschmack überzeugt die Avocado mit Inhaltsstoffen wie Vitamin A und E, gesunden ... [mehr]

Folge 1

Das Wüstenklima

Hitzerekorde der Erde wurden und werden in Wüsten gemessen. Den bisherigen Weltrekord hält Azizia (libysche Wüste) mit fast 58° C im Schatten. Aber auch das Death Valley in den USA mit 56,7° C und Queensland ... [mehr]

Folge 2

Wüstentypen

Wüsten umfassen rund 15 % der gesamten Erdoberfläche. Teilweise ziehen sie sich fast wie ein Gürtel um die Erde, teilweise liegen sie an bestimmten Stellen der Kontinente. Die Wüstenforschung hat Erklärungen ... [mehr]

Folge 3

Wüstenformen

Die Verwitterung, der Wind, aber auch das selten fließende Wasser gestalten aus den unterschiedlichen Ausgangsmaterialien verschiedenartige Wüstenformen: Die Sandwüste ist vermutlich jene ... [mehr]

Bananenreifung

Grasgrün sind die Bananen, wenn sie nach drei Wochen Reise in Hartl bei Kaindorf in der Oststeiermark ankommen. Mit einem fruchtigen Knacken bricht Reifemeister Gunar Nakladal einen Finger – so der Fachbegriff ... [mehr]

Die Vermessung des Everest

Der höchste Berg der Welt ist 8848 Meter hoch. Geologen stellen die Höhenangabe aber seit Jahrzehnten infrage. Nun will Nepal Klarheit schaffen: Seit Jahrzehnten ist das fix:
8848 Meter. So hoch ist der ... [mehr]

Europäische Wolkenforschung

Das Sonnblick-Observatorium in Rauris (Pinzgau) wird zum europäischen Zentrum der Wolkenforschung. Die Ergebnisse und entwickelten Messgeräte sollen dann im europaweiten Wetter- und Klimaforschungsprojekt ... [mehr]

Fast-Fashion-Müllberg

Vor der Tür der kleinen Holzhütte stapeln sich tonnenweise Altkleider. Ein gigantischer Müllberg, von dem Manuela Olivos lebt. Sie recycelt den Kleidermüll, der aus der ganzen Welt hierher gekarrt wird. Oft auch ... [mehr]

Fataler Kreislauf

Die tauenden Permafrostböden in der Arktis werden in Zukunft deutlich mehr Treibhausgase freisetzen als bisher angenommen. Verantwortlich dafür ist ein unscheinbarer Effekt mit globalen Folgen ... [mehr]

Lawinengefahr

In Österreich sterben jährlich rund 30 Menschen in Lawinen. Wer sich abseits gesicherter Pisten bewegt, trägt hohe Eigenverantwortung. Hier finden Sie die wichtigsten Tipps für sichere Skitouren. [mehr]

Methanleck im Meeresboden

Im Boden der Antarktis dürfte ein Leck seit Jahren Methan freisetzen – ein Gas, das zum Treibhauseffekt beiträgt. Es handelt sich um das erste aktive Leck von Meeresbodenmethan in der Antarktis ... [mehr]

Muscheldünen

So könnte die Landschaft um Nexing vor 12 Millionen Jahren ausgesehen haben. Geologen fanden Knochen von Delfinen, Robben, urtümlichen Elefanten und Nashörnern. Nexing im Weinviertel ist ein eher ... [mehr]

Neue Rohstoffmächte

Metalle wie Kobalt, Kupfer und Lithium sind für Technologien von Elektroautos bis hin zur Gewinnung erneuerbarer Energie unverzichtbar und könnten Ländern wie Chile, Peru und der Demokratischen Republik (DR) Kongo ... [mehr]

Übersiedlung

Indonesien will in den nächsten Jahren eine gänzlich neue Hauptstadt errichten. Ähnliche Pläne gibt es aktuell auch in Ägypten. Dass Hauptstädte verlegt werden, ist nichts Neues − dahinter steckt meist eine Fülle ... [mehr]

Die Top Ten

Hier finden Sie die aktuellen Top 10 aus der Welt der Geographie. Dabei können Sie zum einen pro IP und pro Tag genau zweimal Ihre Stimme abgeben und zum anderen per E−Mail einen Link vorschlagen. [mehr]

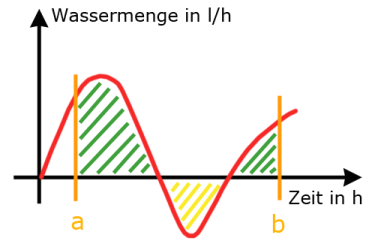Integral

Die LEIBNIZ´sche Schreibweise des lang gezogenen S für das Integralzeichen führt nicht selten zur Interpretation Integrieren bedeutet Summieren. Dabei wird als Einstiegsmodell meist der Flächeninhalt ... [mehr]

Mittelwert

Unter dem Mittelwert (Durchschnittswert) zweier oder mehrerer Zahlen versteht man im allgemeinen das arithmetische Mittel aus allen zu berücksichtigenden Zahlenwerten. Dabei wird die Summe aller ... [mehr]

Primzahl

Eine Primzahl ist eine natürliche Zahl, die genau zwei natürliche Zahlen - nämlich die Zahl 1 und sich selbst - als Teiler besitzt. Das Wort "Primzahl" kommt aus dem Französischen (nombre premier) und bedeutet ... [mehr]

RSA-Algorithmus

Der RSA–Algorithmus wurde im Jahre 1977 von Ron Rivest, Adi Shamir und Leonard Adleman entwickelt. Das Verfahren verwendet große Primzahlen und seine Sicherheit basiert auf der Schwierigkeit, große natürliche Zahlen ... [mehr]

Das HERON´sche Verfahren

Mit Hilfe des nach HERON von Alexandria (um 60 n. Chr.) benannten Verfahrens ist es möglich, die Quadratwurzel einer positiven Zahl ausschließlich mit Hilfe der elementaren Grundrechenoperationen ... [mehr]

Logische Fortsetzung

In vielen Rätselecken findet sich die Zahlenreihe 1-2-4-? verbunden mit der Fragestellung, welche Zahl an Stelle des Fragezeichens "logischerweise" einzusetzen ist. Bei den meisten Zahlenrätseln wird im allgemeinen ... [mehr]

Mit einem Griff

Zufallsexperimente können aus einfachen Zufallsexperimenten, die in einer bestimmten Reihenfolge ablaufen, zusammengesetzt sein. Sie werden in diesem Fall mehrstufige ... [mehr]

Schnell quadriert

Natürliche Zahlen mit der Einerziffer 5 lassen sich − innerhalb eines bestimmten Wertebereiches − relativ einfach in zwei Schritten quadrieren. Zuerst wird der Ziffernblock vor der Einerstelle 5 ... [mehr]

Füllen eines Gefäßes

Der Innenraum eines 20 cm hohen Gefäßes hat in jeder Höhe h eine rechteckige, horizontale Querschnittsfläche. Ihre Länge beträgt am Boden 10 cm und nimmt dann mit der Höhe linear bis auf 16 cm zu ...  [mehr]

Die Umfrage

Ein Cafetier erhält als Ergebnis einer Umfrage zum Thema "Kaffee- und Teekonsum" folgenden Bericht: Von insgesamt 100 Befragten trinken 78 Kaffee, 71 Tee sowie 48 Kaffee und Tee. Der Cafetier lehnt den Bericht als ...  [mehr]

Rechtecke

Zwei deckungsgleiche Rechtecke mit Seitenlängen 3 cm und 9 cm überlappen sich.

Wie groß ist die überlappende (graue) Fläche ? [mehr]

Taschenrechner

Im heutigen Bilderrätsel Taschenrechner entsteht das Gesamtbild durch das Anklicken von genau 4 Zellen, wobei beim Anklicken einer Zelle der Inhalt dieser Zelle sowie der Inhalt der waagrecht und ... [mehr]

Bremsen oder Durchstarten ?

Ein Autofahrer nähert sich bei trockener Fahrbahn und klaren Sichtverhältnissen einer durch Lichtzeichen geregelten Kreuzung.
Ab welcher Entfernung muß er bremsen und bis zu welcher Entfernung kann er ... [mehr]

Das Angebot

Stellen Sie sich folgende Situation vor:
Ein Arbeitgeber bietet Ihnen ein Jahresgehalt von € 10.000,-- und eine regelmäßige Gehaltssteigerung an. Dabei können Sie wählen, ob sie nach jedem Jahr um € 1.000,-- ... [mehr]

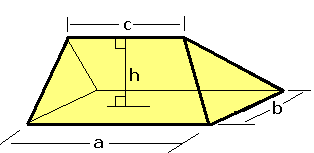Ein Ausflug in die Stereometrie

Einen kleinen Ausflug in die Welt der Stereometrie ermöglicht die folgende CAS-Animation: Ausgangssituation ist ein Quader, der bekanntlich durch insgesamt sechs Rechtecke, die paarweise ... [mehr]

Kraut und Rüben

Ein Landwirt möchte 45 Hektar Ackerland mit Weizen und Zuckerrüben bebauen. Die erforderliche Arbeitszeit beträgt beim Weizenanbau 20 Stunden pro Hektar, beim Zuckerrübenanbau 50 Stunden ... [mehr]

Maschendrahtzaun

Ein Grundstücksbesitzer besitzt einen Maschendrahtzaun mit einer Länge von 80 Meter. Er möchte damit ein rechteckiges Gehege einrichten. Wie sind Länge und Breite des Geheges zu wählen, damit ... [mehr]

Dynamische Renten

Das Kernstück der Finanzmathematik ist die Berechnung von Renten, wobei die "klassische" Definition einer Rente besagt: "Eine Rente ist eine Folge von Zahlungen in gleicher Höhe und in gleichen Zeitabständen." [mehr]

Schüttung eines Brunnens

Ein Hausbesitzer ärgert sich über die ständigen Preiserhöhungen seines Leitungswassers.
So bohrt er sich im späten Frühjahr einen Brunnen in seinem Garten und pumpt aus diesem täglich die maximal ...  [mehr]

Textverschlüsselung

Die Kryptologie oder Kryptographie beschäftigt sich vorwiegend mit dem Ver- und Entschlüsseln von Nachrichten und Botschaften. Dabei wird generell zwischen symmetrischen (ein- und ... [mehr]

Alle Lichter

Bei diesem Extra sollen durch das Anklicken einiger Zellen alle Zellen eingefärbt werden. Dabei wird beim Anklick einer Zelle deren Farbe sowie die Farbe aller waagrecht und senkrecht benachbarten Zellen verändert. [mehr]

Chuck a Luck

Chuck a Luck ist ein einfaches Würfelspiel. Eine Spieler[in] setzt auf eine der sechs Zahlen, danach werden drei Würfel geworfen.
Zeigen genau 1 ≤ k ≤ 3 Würfel die gesetzte Augenzahl, so wird der k-fache ... [mehr]

Drei Türen

Mit dieser NMS-Online-Applikation haben Sie die Möglichkeit, das mittlerweile bekannte und auch populäre Ziegenproblem nachzuspielen, wobei die Anzahl der Runden pro User[in] mit 99 beschränkt ist. Zusätzlich ... [mehr]

Dreimal eine Frage

Bei diesem Kartenspiel kann durch eine einzige Frage, die dreimal nacheinander gestellt und auch richtig beantwortet werden muss, aus einem Kartenpaket von 3 x 7 = 21 Karten eine zu Beginn gedanklich ... [mehr]

Ja oder Nein

Hier kann aus einem Kartenpaket von 31 Karten eine zu Beginn gedanklich markierte Karte durch eine einzige Entscheidungsfrage, die fünfmal nacheinander gestellt und auch richtig beantwortet werden muss, ... [mehr]

Roulette

Roulette ist das am weitesten verbreitete Glücksspiel, das in Spielbanken angeboten wird. Ziel dieses Spiels ist die Vorhersage einer Glückszahl aus den insgesamt 37 möglichen Zahlen von 0 bis 36. Dazu können ... [mehr]

Schatzsuche

Beim Öffnen dieser Seite wird in einem der 20 x 10 = 200 Felder ein Schatz versteckt, welcher mit Hilfe der jeweiligen Angabe des Abstandes (kürzester Weg zum Schatzfeld) durch maximal vier Versuche ... [mehr]

Seven Eleven

Seven Eleven ist ein Würfelspiel, bei dem auf das Eintreffen bzw. Nicht-Eintreffen bestimmter Ereignisse gesetzt werden kann. Insgesamt stehen zwanzig verschiedene Chancen, die mit unterschiedlichen ... [mehr]

Telepathie

Das Wort "Telepathie" (engl. telepathy) ist eine Bezeichnung für die Übertragung von Informationen zwischen Lebewesen ohne Beteiligung bekannter Sinneskanäle oder physikalischer Wechselwirkungen ... [mehr]

Faire Teilung

Zwei Brüder erbten eine Herde Schafe, die sie zur Gänze verkauften. Sie bekamen für jedes Schaf genauso viele Euro wie Schafe in der Herde waren. Der Gesamtbetrag wurde in € 10,-- Scheinen und einigen ... [mehr]

Jack und Jim

Jack und Jim laufen mit gleich bleibender Geschwindigkeit auf einen 440 Meter hohen Berg und wieder zurück. Jack erreicht als Erster den Gipfel und trifft auf seinem Rückweg Jim 20 Meter unterhalb des Gipfels. Jim ... [mehr]

Langes Turnier

Vier Schülermannschaften trugen ein Hallenturnier aus, wobei jede Mannschaft genau einmal gegen jede andere Mannschaft spielte. Jedes Spiel dauerte zweimal 20 Minuten. Nach jeder Halbzeit wurden ... [mehr]

Marillenknödel

Vier Ehepaare treffen sich zu einem fröhlichen Essen. Dabei werden herrliche Marillenknödel serviert und alle acht Personen essen - da die Marillenknödel wunderbar schmecken und auch nicht allzu groß sind - ... [mehr]

Schwieriger Weg

Ein Pferd muss eine bestimmte Strecke zurücklegen. Die erste Hälfte des Weges läuft das Pferd mit einer durchschnittlichen Geschwindigkeit von 12 km/h, den restlichen Weg, weil es einen schweren ... [mehr]

Viele Tunnels

Die Gotthardbahn, eine der bedeutendsten Gebirgsbahnen Europas, hat eine Tunnelzahl, welche um zwölf größer als deren Gesamtlänge in Kilometern ist. Dabei ist der Haupttunnel allein so lang, daß seine ... [mehr]

Zwei Uhren

Zwei Freunde wollen sich um 17 Uhr beim Hauptplatz treffen. Bernhards Uhr geht zehn Minuten nach, er glaubt jedoch, sie gehe fünf Minuten vor. Olivers Uhr dagegen geht fünf Minuten vor, ... [mehr]

Zwei Zahlen

Martina und Martin sollten zwei verschiedene Zahlen miteinander multiplizieren. Zur Probe dividierten sie ihr Ergebnis durch die größere der beiden Zahlen, was jedoch bei beiden nicht stimmte. Martina erhielt ... [mehr]

Baumstammlänge

Ein Traktor zieht einen Baumstamm mit konstanter Geschwindigkeit. Ein Fußgänger, der an der Länge des Baumstammes interessiert ist, geht zuerst in gleichmäßigen Schritten vom rückwärtigen zum vorderen ... [mehr]

Bücherwurm

Ein zehnbändiges Lexikon steht in einem Regal. Jeder Band besitzt einen Papierteil mit einer Dicke von 4,5 cm und einen Ledereinband, der auf jeder der beiden Seiten 0,5 cm dick ist. Ein Bücherwurm frisst sich auf ... [mehr]

Das Schlagzeug

Ein junger Mann möchte in einer Siedlung Zeitungsabonnements verkaufen und erklärt: "Ich bin Mathematikstudent und muss mir das Geld für mein Studium durch Zeitungsverkäufe verdienen. Bitte helfen Sie mir, ... [mehr]

Der richtige Weg

Ein Weltumsegler befindet sich auf einer Insel, die von zwei Stämmen, deren einer nur lügt und deren anderer nur die Wahrheit sagt, bewohnt wird. Er gelangt nun zu einer Wegverzweigung und muss einen Eingeborenen ... [mehr]

Die Mütze

Ein Schwimmer springt von einer Brücke in einen Fluss und beginnt, gegen die Strömung des Flusses zu schwimmen. Unmittelbar vor dem Eintauchen ins Wasser verliert er seine Baseballmütze. Nachdem er ... [mehr]

Die Rolltreppe

Ein Student möchte die Stufenzahl einer Rolltreppe bestimmen. Dazu geht er zunächst die Rolltreppe in Fahrtrichtung entlang und zählt dabei insgesamt 90 Stufen. Anschließend geht er die Rolltreppe entgegen der ... [mehr]

Ein Cent

Nichts ist anspornender als das Schätzen von Ergebnissen, und gerade dieser Denksport-Klassiker zeigt recht deutlich, wie sehr sich die Ergebnisse bei einer kleinen Änderung der Ausgangssituation - in diesem Fall ... [mehr]

Ein Königsrätsel

Ein König wollte einem Gefangenen noch eine Chance geben, frei zu kommen. Dazu stellte er ihm folgende Aufgabe: "Ich habe hier genau ein Dutzend Münzen. Jede Münze trägt auf der Vorderseite mein Antlitz und ... [mehr]

Ein Schachturnier

Acht Personen nehmen an einem Schachturnier teil, wobei jede[r] gegen jede[n] genau eine Partie spielt. Jeder Sieg wird mit einem Punkt, jedes Remis mit einem halben Punkt belohnt. Am Ende ist der Rangtabelle zu ... [mehr]

Eine Schafherde

Als man einen Schäfer nach der Zahl seiner Schafe fragte, gab er zur Antwort: "Wenn ich von meinen Schafen die Hälfte und ein halbes verkaufen würde, dann von dem Rest wieder die Hälfte und ein halbes, und das ... [mehr]

Falsche Sätze

Auf einem Blatt Papier stehen folgende 100 Sätze: "Genau ein Satz auf diesem Blatt ist falsch.", "Genau zwei Sätze auf diesem Blatt sind falsch.", "Genau drei Sätze auf diesem Blatt sind falsch.", "Genau vier Sätze auf ..." [mehr]

Familiengrösse

Ein Junge hat ebenso viele Schwestern wie Brüder und jede seiner Schwestern hat halb so viele Schwestern wie Brüder. Wie viele Brüder und Schwestern gibt es in dieser Familie ? [mehr]

Fehlender Schilling

Klassiker haben bekanntlich ein bestimmtes Alter - und so verwundert es auch nicht, wenn in der folgenden Aufgabe die frühere österreichische Währungseinheit "Schilling" zum Einsatz kommt.
Drei Schüler kaufen gemeinsam ... [mehr]

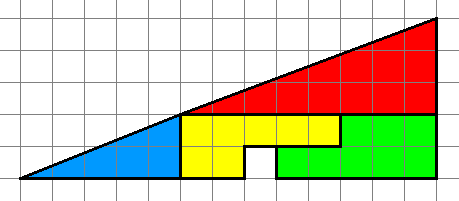Figuren

Aus zwei rechtwinkeligen Dreiecken und zwei Sechsecken entstehen durch verschiedene Zusammenlegungen zwei Figuren. Dabei ist bei der zweiten Figur offensichtlich eine Lücke sichtbar. Woher stammt dieser ... [mehr]

Gefälschte Münzen

Aus den zahlreichen Wägeproblemen sei an dieser Stelle ein Klassiker mit einer verblüffend einfachen Lösung angeführt: Man hat 10 Haufen von Münzen und jeder Haufen enthält 10 Centstücke. Ein gesamter Haufen ... [mehr]

Handschuhe

Michaela möchte an einem kalten Wintertag einen Spaziergang unternehmen. Daher greift sie (blind) in eine Schublade, in der sich vier dunkelblaue, sechs dunkelrote und acht scharze Strickhandschuhe befinden, ... [mehr]

Kaffee oder Tee ?

Michaela möchte an einem kalten Wintertag einen Spaziergang unternehmen. Daher greift sie (blind) in eine Schublade, in der sich vier dunkelblaue, sechs dunkelrote und acht scharze Strickhandschuhe befinden, ... [mehr]

Kamelleasing

Ein alter Beduine hinterlässt seinen drei Söhnen 17 Kamele. Das Testament bestimmt, daß der älteste Sohn die Hälfte, der mittlere ein Drittel und der jüngste ein Neuntel der Erbmasse erhalten soll. Ein geliehenes Kamel ... [mehr]

Kurz und bündig

Gemeinsam mit seinem Dackel strebt ein Oberförster nach erfolgreicher Pirsch dem heimatlichen Forsthaus zu. Exakt 270 Meter vor dem Haus lässt er seinen Dackel von der Leine, welcher freudig bellend auf die ... [mehr]

Letzte Chance

Vier Männer wurden in Mathematanien zum Tode verurteilt. Der Chef des Exekutionskommandos möchte ihnen jedoch noch eine Chance geben und sagt: "Ich grabe euch jetzt alle vier in einer Reihe so in den Wüstensand ein ... [mehr]

Mehr oder weniger ?

Mario und Luigi möchten 2 kg Zucker abwiegen, haben jedoch nur eine Balkenwaage mit zwei ungleich langen Armen. Da hat Luigi eine Idee: Er legt ein 1 kg-Gewicht auf die eine Schale der Waage und schüttet in die andere ... [mehr]

Obstanbau

Eine Landjugend half beim Bepflanzen einer Obstplantage, dazu veranstaltete der Bauernbund einen Wettbewerb mit drei Mannschaften A, B und C. Alle waren fleißig bei der Arbeit, da wären sie beinahe ... [mehr]

Papierfalten

Ein (genügend grosses) Blatt Papier besitzt eine Dicke von 0,1 mm. Wie oft muss dieses Blatt jeweils in der Mitte gefaltet und anschließend zusammengelegt werden, um von der Erde auf den Mond (mittlere Entfernung ... [mehr]

Reifenpanne

Als ein Radfahrer zwei Drittel seines Weges zurückgelegt hatte, platzte ein Reifen. Für den Rest des Weges benötigte er zu Fuß doppelt so lange wie für die bisherige Fahrt mit dem Rad. Wie verhalten sich seine Radfahr- ... [mehr]

Schneckentempo

Eine Schnecke möchte eine Höhendifferenz von 10 Meter überwinden. Dabei bewältigt sie tagsüber eine Höhendifferenz von zwei Meter, während sie in der Nacht wieder um einen Höhenmeter abrutscht. Wann ... [mehr]

Seerosen

In einem Teich mit einer Wasseroberfläche von 3000 m² befindet sich eine Seerosenpopulation, deren Größe sich täglich verdoppelt. Nach 15 Tagen ist exakt die Hälfte der Teichoberfläche mit Seerosen bedeckt. Nach wie ... [mehr]

Sturmschaden

Am Rande eines 3 Meter breiten Grabens steht ein 9 Meter hoher Baum. Ein Sturm knickt den Baum an einer Stelle, sodaß die Spitze des Baumes gerade die andere Seite des Grabens berührt. In welcher Höhe ist ... [mehr]

Tourismus

Eine Touristengruppe wird von einem Ortskundigen durch ein Tal zu einem Hinterhalt geführt. Der Aufbruch beginnt um 6 Uhr morgens bei der Schlangengrube. Nach zwei Stunden fragt ein unruhiger Tourist, wie weit ... [mehr]

Vertrocknete Erdbeeren

Mit diesem Klassiker können nicht wenige Leute in Verlegenheit gebracht werden, denn das Ergebnis ist derart verblüffend, sodaß man zunächst durchaus glauben kann, sich verrechnet zu haben: Ein Händler besitzt am ... [mehr]

Viele Busse

Von einem Bahnhof A fährt zu jeder Viertelstunde ein Bus ab und trifft nach zwei Stunden in einem Bahnhof B ein. Vom Bahnhof B fahren ebenfalls im 15 Minuten−Takt Busse auf ... [mehr]

Viele Kuchen

"Ich habe die Kuchen in die Küche gebracht", sagt Stefan zu seiner Frau, "drei verschiedene Sorten zu € 1,20, € 1,40 und € 1,70. Insgesamt habe ich genau € 2,-- bezahlt." "Sehr gut", sagt seine Frau, die gerade in ... [mehr]

Weiter Weg

Eine Schallplatte mit einem Durchmesser von 34 Zentimetern hat einen nicht bespielten äußeren Rand von zwei Zentimetern und eine nicht bespielte Mittelfläche von zehn Zentimetern Durchmesser. Wenn es pro ... [mehr]

Zwei Ergebnisse

Zwei Fussballmannschaften A und B trugen zwei Spiele aus, wobei insgesamt 13 Tore geschossen wurden. Das erste Spiel endete unentschieden. Im zweiten Spiel fielen mehr Tore als im ersten Spiel, wobei Mannschaft A ... [mehr]

Zwei Rennboote

Zwei Rennboote durchqueren einen See an seiner breitesten Stelle. Sie verlassen gleichzeitig die gegenüber liegenden Ufer, fahren ständig mit jeweils gleichbleibender Geschwindigkeit hin und her und halten an keinem der ... [mehr]

Zwei Schafherden

Als sich zwei Schäfer über ihre Schafherden unterhielten, sagte der erste: "Wenn Du mir acht von Deinen Schafen gibst, dann hat meine Herde genau doppelt so viele Schafe wie Deine Herde." Daraufhin meinte der zweite ... [mehr]

Leonhard EULER

Leonhard EULER (* 15. 4. 1707 in Basel,† 18. 9. 1783 in Petersburg) war ein Schweizer Mathematiker und studierte neben Mathematik auch Theologie, Medizin und orientalische Sprachen. Er kam mit 20 Jahren ... [mehr]

Leonardo FIBONACCI

Der Italiener Leonardo da PISA (ca. 1180 - 1250) - er selbst nannte sich Filius Bonacci, weshalb er heute vorwiegend als Fibonacci bekannt ist - war einer der berühmtesten Mathematiker des Mittelalters. Er ... [mehr]

Carl Friedrich GAUSS

Carl Friedrich GAUSS (* 30. 4. 1777 in Braunschweig, † 23. 2. 1855 in Göttingen) war ein deutscher Mathematiker, Astronom und Physiker. Er veröffentlichte grundlegende Werke über die höhere Arithmetik, die ... [mehr]

Blaise PASCAL

Blaise PASCAL (* 19. 6. 1623 in Clermont-Ferrand, † 19. 8. 1662 in Paris) war ein französischer Philosoph und Naturwissenschaftler. Schon als Kind galt PASCAL als mathematisches ... [mehr]

20 + 20 = 44

"Von 2018 bis 2021 konnten wir unsere Verkaufszahlen um 20 % erhöhen und von 2021 bis 2024 nochmals um 20 %." verkündet der Filialleiter einer Schuhmarktkette stolz vor seinen Angestellten und fährt fort ...  [mehr]

Drohender Verkehrskollaps

In der ORF-Sendung "Zeit im Bild" wurde am 22. Mai 2007 im Beitrag "Verkehrskollaps droht - bis 2030 werden 50 % mehr Autos unterwegs sein" folgende Information verlautbart: "Die Zahl der neuzugelassenen PKW wird bis ... [mehr]

Ein bisschen mehr

Getreu dem Motto "Darf´s ein bisschen mehr sein ?" eine Aufgabe, die eine Verbindung zwischen der Prozentrechnung und dem Auflösen linearer Gleichungssysteme darstellt. Eine Gesellschaft bezahlt in ... [mehr]

Satte Rabatte

Wer kennt nicht den Slogan "Satte Rabatte ! Diesen Freitag und Samstag gibt es minus 25 % auf alle (…) Produkte. Und beim Einlösen des Rabattsammlers gibt es nochmals bis zu minus 20 %. Das sind dann (...) viele ... [mehr]

Saure Mischung

Eine Schüler[innen]gruppe möchte im Rahmen eines Tages der "offenen Tür" eine Mischung aus den beiden Salzen "Ursalz" und "Zitronica" anbieten. Im Rahmen erster Vorbereitungen wurde bereits eine 100 dag ... [mehr]

Teuerungswelle

Im Zuge der Diskussion über die ständig größer zu werdenden Preissteigerungen präsentierte der Ö3-Mikromann am 18. Juli 2008 im Ö3-Wecker folgende Antworten auf die Frage: "Wenn ein Produkt heute doppelt so teuer ... [mehr]

Werbeaktion

Eine Parfümerie macht ihren Kundinnen und Kunden im Rahmen einer Werbeaktion folgendes Angebot: "Bei einem Einkauf von zwei Produkten zu einem Gesamtpreis von – mindestens - € 80,-- erhalten Sie 15 % ...[mehr]

Basis und mehr

Mit diesem Quiz können Sie Ihr Wissen im Bereich der mathematischen Grundlagen unter Beweis stellen. 15 Fragen auf dem Weg zum Gipfel, natürlich mit den drei bekannten Jokern, jedoch ohne zeitliches Limit. [mehr]

Wahrscheinlichkeiten

Von der richtigen Anzahl fünfstelliger Telefonnummern über die Dauer von Sitzanordnungen bis hin zum sicheren Urteil eines bellenden Spürhundes finden Sie hier so manch "kuriose" ... [mehr]

Biorhythmus

Der Biorhythmus ist eine Hypothese, nach der die physische und die intellektuelle Leistungsfähigkeit sowie der Gemütszustand eines Menschen bestimmten Rhythmen, die mit dem Tag der Geburt beginnen, ... [mehr]

Ewiger Kalender

Wer hat sich nicht schon einmal gefragt, an welchem Wochentag er geboren wurde, an welchem Wochentag sein 50. Geburtstag sein wird oder auf welchen Tag im nächsten Jahr der Heilige Abend fällt. Ausgangspunkt ... [mehr]

Online-Rechner

Hier finden Sie einen Online-Rechner mit den wichtigsten mathematischen Funktionen.
Weitere Hinweise zum richtigen Einsatz dieses Rechners erhalten Sie nach Betätigen der Info-Taste. Alle ... [mehr]

Ostern und mehr

Auf dem Konzil von Nizäa, einer Zusammenkunft von Bischöfen und anderen Amts- und Würdenträgern, wurde im Jahr 325 n. Chr. für die gesamte Christenheit festgelegt, daß das Osterfest ... [mehr]

Prozentrechner

Mit Hilfe dieses Prozentrechners können Sie wahlweise eine der drei Größen Grundwert, Prozentsatz und Prozentwert berechnen, wenn die beiden anderen gegeben sind. Dabei werden ... [mehr]

Rentenrechner

Mit Hilfe dieses Rentenrechners können Sie wahlweise eine der Größen Barwert, Rentenrate, Endwert, Rentenlaufzeit und Rentenzinssatz berechnen. Beachten Sie dabei bitte, daß sämtliche ... [mehr]

Folge 1

Um den Äquator 1

In der ersten Folge wird der exakte Lösungsweg des durchaus bekannten Denksport-Klassikers gezeigt. Zu Beginn jedoch zur Erinnerung die Aufgabenstellung: Ein Seil wird straff um den Erdäquator gespannt und ... [mehr]

Folge 2

Um den Äquator 2

Wie sehr sich eine kleine Änderung der Aufgabenstellung auf den Wert des Ergebnisses auswirken kann, zeigt diese Folge. Zunächst wiederum die Aufgabenstellung: Ein Seil wird straff um den Erdäquator gespannt ... [mehr]

Folge 3

Vom Nordpol zum Südpol

Wie sehr sich eine kleine Änderung der Aufgabenstellung auf den Wert des Ergebnisses auswirken kann, zeigt diese Folge. Zunächst wiederum die Aufgabenstellung: Ein Seil wird straff um den Erdäquator gespannt ... [mehr]

Folge 1

Die Kandidaten-Methode

Ein magisches Quadrat der Grösse 4 x 4 findet sich bereits im Jahre 1514 im Kupferstich "Melencolia" von Albrecht Dürer. In diesem Quadrat besitzen nicht nur Zeilen-, Spalten- und Diagonalsumme, sondern auch ... [mehr]

Folge 2

Die allgemeine Methode

Um zu einer vorgegebenen (genauer: beliebigen, jedoch über 34 liegenden natürlichen) Summenzahl ein magisches Quadrat zu erstellen, können prinzipiell folgende drei Varianten (einzeln oder in kombinierter Form) ... [mehr]

Folge 3

Die sichere Methode

Für die Erstellung eines magischen Zahlenquadrates mit einer vorgegebenen Zeilen-, Spalten- und Diagonalensumme kann − in Anlehnung an die Kandidaten-Methode − das Basisquadrat ... [mehr]

Folge 1

Schachfinale

Als einführendes Beispiel ein Rätsel zum Thema "Schachfinale", das auch bei Nichtkenntnis des Schachspiels mit Hilfe einer Tabelle gelöst werden kann: Im Finale des Schachturniers eines Clubs trafen ... [mehr]

Folge 2

Undercover

Eine durchaus einfache Logik-Aufgabe, die mit Hilfe eines Diagrammes gelöst werden kann:
Seit Wochen arbeiten Beamte einer Sonderkommission als verdeckte Ermittler in Lokalen, um einer ... [mehr]

Folge 3

Einstein´s Rätsel

Das folgende Rätsel wird häufig Albert Einstein zugeschrieben, der gleichzeitig behauptet haben soll, daß 98 % der Weltbevölkerung nicht in der Lage seien, es zu lösen. Zuerst die Ausgangssituation: Es gibt ... [mehr]

Folge 1

Die Fingermultiplikation

Daß die Addition zweier natürlicher Zahlen mit Hilfe der menschlichen Finger durchgeführt werden kann, ist allgemein bekannt.
Aber selbst die Multiplikation zweier natürlicher Zahlen läßt sich − wenn auch ... [mehr]

Folge 2

Die Kreuzmultiplikation

Ausgangspunkt für diese Folge ist die Multiplikation einer zweistelligen Zahl, die eine einstellige Ziffernsumme besitzt, mit dem Faktor 11. Dabei zeigt sich, daß beim gesuchten Produkt zwischen der ersten ... [mehr]

Folge 3

Die vedische Multiplikation

Es wäre durchaus nicht übertrieben, dieser Folge den Werbeslogan "Frag´ doch den Inder" als Titel zu geben, denn die vedische Multiplikation ist ein aus Indien stammendes Rechenverfahren.
So kann etwa die Multiplikation ... [mehr]

Folge 4

Verdoppeln und Halbieren

Für die Multiplikation zweier natürlicher Zahlen kann auch das folgende − bereits im alten Ägypten angewendete und im folgenden anhand der Multiplikation 45.67 vorgestellte − Verfahren, das genau genommen nur ... [mehr]

Folge 1

Spielbedingungen

Der österreichische Joker ist im Sinne des Gesetzes eine Ausspielung, die nur in Verbindung mit Lotto-, EuroMillionen-, Toto-, Zahlenlotto-, Zahlenlotto "TopTipp" und Bingo-Wetten sowie ... [mehr]

Folge 2

Gewinnerwartung

Für die Berechnung der Gewinnerwartung ist zu Beginn ein Blick in die (aktuelle) Gewinntabelle nötig. Nun wird diese Tabelle durch beiden Spalten "Chance" und "Gewinnerwartung" ergänzt. [mehr]

Folge 3

Ziehungsverfahren

Für die Ermittlung der Jokerzahl wird ein Ziehungsgerät, das sechs voneinander getrennte Kammern besitzt, verwendet. In jeder dieser Kammer befinden sich zehn Kugeln, die mit den Ziffern 0 bis 9 beschriftet sind. Bei der ... [mehr]

Folge 4

Statistik

Von der klassischen Suche im Ziehungsarchiv über verschiedene Auswertungen zu Häufigkeitsverteilungen bis zur Suche nach dem letzten Ziehungsdatum einer oder mehrerer Stellen einer Jokerzahl. Diese ... [mehr]

Folge 1

Spielbedingungen

Das österreichische Lotto "6 aus 45" ist im Sinne des Gesetzes eine Ausspielung, bei der ein Veranstalter Wetten über die Gewinnchancen mehrerer Zahlen aus einer bestimmten Zahlenreihe annimmt und ... [mehr]

Folge 2

Gewinntabelle

Die vermutlich am häufigsten gestellte Frage beim Lotto "6 aus 45" lautet: "Mit welcher Wahrscheinlichkeit hat man mit einem Lotto-Tipp sechs Richtige ?"
"Sechs Richtige" hat ein ... [mehr]

Folge 3

Systemspiele

Beim Systemspiel, das in erster Linie eine Abkürzung für verschiedene Zahlenkombinationen darstellt, können mehr als sechs Zahlen angekreuzt werden. Dabei wird zwischen Bankzahlen, die in ... [mehr]

Folge 4

Nachbarn beim Lotto

Bei der Ziehung der Lottozahlen stellt so manche[r] Spielteilnehmer[in] fest, daß getreu dem Motto "Knapp daneben ist auch vorbei." eine oder mehrere der sechs Gewinnzahlen auf dem Spielschein unmittelbar ... [mehr]

Folge 5

Tausend Tipps

Daß bei einer Spielrunde des Lotto "6 aus 45" die Chance auf "6 Richtige" mit der Anzahl der abgegebenen (und verschiedenen) Tipps steigt, ist eine Binsenweisheit. Wird jedoch mehr als ein Lotto-Tipp gespielt, so können ... [mehr]

Folge 6

Statistik

Von der klassischen Suche im Ziehungsarchiv über verschiedene Auswertungen zu Häufigkeitsverteilungen bis zur Suche nach dem letzten Ziehungsdatum einer oder mehrerer Gewinnzahlen. Diese Plattform ... [mehr]

Folge 1

Aussichtslose Lage

"Alles, was ich sage, ist gelogen", behauptet ein von seinen lügnerischen Fähigkeiten restlos überzeugter Lügner. Aber kann man ihm diesen Satz tatsächlich glauben ? Um diese Frage zu beantworten, kann eine ... [mehr]

Folge 2

Der sichere Hang

Nicht selten führen Aufgaben aus dem Gebiet der "bedingten Wahrscheinlichkeit" zu einem Trugschluss, weshalb an dieser Stelle ein Beispiel mit einem durchaus erstaunlichen Ergebnis angeführt sei: Ein Hang kann an ... [mehr]

Folge 3

Die Mücke und der Elefant

Ausgangspunkt für diesen Trugschluss–Klassiker ist das Festlegen der Variablen x (Gewicht der Mücke) und y (Gewicht des Elefanten).
Zusätzlich kann die Summe der beiden Gewichte durch den Term 2z ... [mehr]

Folge 4

Etwas voreilig

Ein junger Verehrer möchte dem von ihm heiß begehrten Fräulein einen prächtigen Strauß roter Rosen zum Geburtstag überreichen. Auf sein Klingeln wird ihm aber nicht geöffnet. Enttäuscht fragt er bei der Nachbarin nach ... [mehr]

Folge 5

Schwieriger Verkauf

Zwei Frauen wollen auf dem Wochenmarkt jeweils 30 Stück Bananen verkaufen. Die erste Frau verlangt für zwei Bananen € 0,50 Cent, die zweite Frau für drei Bananen € 1,--. Somit hofft die erste Frau auf eine ... [mehr]

Folge 6

Völlig verzweifelt

Während seines Urlaubs in einem kleinen Dorf läßt sich ein Gast vom dortigen Friseur rasieren. "Na, wie gehen denn die Geschäfte ?", fragt er den Friseur. "Danke, ich bin zufrieden und kann mich nicht beklagen", antwortet ... [mehr]

Folge 1

Jungen und Mädchen 1

Für das erste Würfelspiel dieser Serie werden zwei Wurfbeispiele angegeben: Das erste Wurfbild besitzt die Interpretation "Ein Junge und zwei Mädchen besitzen € 8,--.", während das zweite Wurfbild mit dem Satz ... [mehr]

Folge 2

Jungen und Mädchen 2

Sollte das Prinzip des ersten Würfelspiels bereits bekannt sein, so heißt es zu Beginn dieses Würfelspiels unbedingt "Vorsicht !". Denn auch diesmal dreht es sich um Jungen, Mädchen und Euros, jedoch ist der ... [mehr]

Folge 3

Inuit und Fische

In dieser Folge wird einer der seltsamsten Zusammenhänge zwischen Würfelergebnis und Interpretation verwendet, weshalb zu Beginn − getreu dem Sprichwort "Aller guten Dingen sind drei." - auch drei ... [mehr]

Das aktuelle Su Doku-Rätsel

Die täglich aktualisierten Su Dokus für heute,
Donnerstag, den 3. April 2025
in drei verschiedenen Schwierigkeitsgraden und in drei verschiedenen Grössen (4 x 4, 6 x 6 und 9 x 9). [mehr]

Su Doku-Solver

Mit Hilfe dieses Su Doku-Solvers kann nach Eingabe einzelner Werte ein vollständiges Su Doku in den Größen 4 x 4, 6 x 6 und 9 x 9 erstellt werden. Lässt sich mit Hilfe der eingegebenen Werte ein eindeutiges ... [mehr]

Achill und die Schildkröte

Vor knapp 2500 Jahren stellte der griechische Philosoph Zenon von Elea folgendes Problem auf: "Der schnellfüssige Achilles folgt einer Schildkröte, die sich ein Stadion (rund 180 Meter) vor ihm befindet. Er ...  [mehr]

Bescheidener Wunsch

Die wohl berühmteste Legende um die Entstehung des Schachspiels stammt aus alten arabischen Quellen. Danach soll der brahmanische Weise Sissa ibn Dahir das Schachspiel zur Belehrung ... [mehr]

Das Haltestellenbeispiel

Fast schon ein Klassiker für den Einstieg in die Materie der Wahrscheinlichkeitsrechnung ist das Haltestellenbeispiel: Ein Student wohnt in der Nähe einer Haltestelle einer Lokalbahn, die in der einen Richtung zur ... [mehr]

Der feine Unterschied

Auf so manchem Leipziger Strassenbahnwagen stand noch bis vor geraumer Zeit der Text "Auf- oder Abspringen während der Fahrt polizeilich verboten !". Deutlich ist dabei zu erkennen, daß unter dem Wörtchen "oder" ... [mehr]

Money Maker

In der Sendung "Money Maker" (in den Sommermonaten Juli und August im TV-Vorabendprogramm) können zwei Kandidat[inn]en um den Gewinn eines "Wiener Philharmonikers" spielen. Dabei ... [mehr]

Rollende Staukolonne

Jeden Sommer häufen sich Meldungen über Staus und lange Wartezeiten vor dem Tauerntunnel der A 10 (Tauernautobahn). Nicht nur für Verkehrsplaner stellt sich dabei die Frage, mit welcher ... [mehr]

Teilbarkeiten

Eine erste Anwendung des Begriffes "Teilbarkeit" findet sich in der Bruchrechnung, wenn bei Addition und Subtraktion ungleichnamiger Brüche ein kleinster gemeinsamer Nenner zu suchen ist und dieser mit ... [mehr]

Tempo, Tempo

Am 13. Juli 2009 wurde auf der Homepage von Radio Salzburg unter dem Titel "Streit um Grünphase bei Fußgängerampel" folgende Meldung veröffentlicht: Eine Fußgängerampel in der Stadt Salzburg sorgt für ...  [mehr]

Themenpool

Bei der mündlichen Reifeprüfung zieht jede*r Prüfungskandidat*in zwei Themenbereiche aus einem zuvor von der jeweiligen Lehrperson erstellten Themenpool. Danach wählt der/die ... [mehr]

Vertauschte Briefe

Eine Sekretärin schreibt fünf Briefe (mit verschiedenem Inhalt) und adressiert fünf Umschläge (mit verschiedenen Adressen). Anschließend steckt sie jeweils einen Brief - ohne auf die jeweilige Adresse zu ... [mehr]